Resuelta la duda en Isla Twyfel.

Tras contaros en "el programa del pasado domingo" la llegada de Callejeros Viajeros a Isla Twyfel (la isla de la duda, como su nombre indica), "este domingo llega al programa" Callejeros Viajeros resuelve el misterio de Isla Twyfel: qué tribu era la que siempre mentía y qué tribu era la que siempre decía la verdad.

Recordemos la situación del reportero con los jefes de las tribus:

"[...] el reportero que no pudo disfrutar del recibimiento preguntó al jefe de la pluma verde:

- ¿Es usted el jefe de la tribu que dice la verdad?

- Ups -respondió el nativo.

El reportero reconoció de inmediato el término nativo ups, que quería decir sí. ¿O quería decir no? No lo tenía claro.

- Dijo “sí” –replicó el nativo de la pluma roja- ¡pero él gran mentiroso! [...] "

 

RESOLVÁMOSLO:

Priper paso: La palabra "ups" solo puede significar SÍ.
Analicemos la situación:
Tenemos dos opciones: El Pluma Verde dice la verdad o miente.
Si dice la verdad (es de la tribu de los que dicen la verdad), contestaría sí a la pregunta y por tanto "ups" significará sí.
Si miente (pertenece a la tribu de los que mienten) contestará (mintiendo como siempre) a la pregunta diciendo que sí que pertenece a la tribu de los que dicen la verdad. Luego "ups" vuelve a significar sí.

Segundo paso:
Cuando el Jefe Pluma Roja dijo que "ups" significaba sí, decía la verdad, pues como hemos visto en el paso anterior "ups" solo puede significar sí.

Por tanto LOS PLUMA VERDE SON GRANDES MENTIROSOS, y LOS PLUMA ROJA MUY SINCEROS.

Callejeros viajeros en Isla Twyfel

Los reporteros de Callejeros viajeros llegaron a Isla  Twyfel con el objetivo de grabar la vida de las 2 tribus muy curiosas que vivían allí. De ellas sabían que aunque convivían en un mismo lugar, los miembros de una de las tribus siempre decían la verdad, y los de la otra siempre mentían.

Al llegar allí uno de los reporteros se reunió con los jefes de las tribus, mientras el resto disfrutaba de las danzas de recibimiento que las tribus habían preparado.

 Uno de los jefes llevaba una gran pluma verde en la cabeza, el otro una pluma roja en el cuello.

 Para poder realizar los reporteros su reportaje debían averiguar qué tribu siempre mentía y cuál decía la verdad. Para ello el reportero que no pudo disfrutar del recibimiento preguntó al jefe de la pluma verde:

-          ¿Es usted el jefe de la tribu que dice la verdad?

-          Ups  -respondió el nativo.

El reportero reconoció de inmediato el término nativo ups, que quería decir sí. ¿O quería decir no? No lo tenía claro.

-          Dijo “sí” –replicó el nativo de la pluma roja- ¡pero él gran mentiroso!

Gracias a esa intervención del nativo de pluma roja pudo saber a qué tribu representaba cada uno de los jefes.

 

¿Y tú, lo sabes? (lógica matemática)

Deja tu comentario y en unos días te cuento…

Calendario Matemático... (Noviembre)

Y llegó noviembre... Y como en la vida misma, ¡cada día de noviembre hay matemáticas!

Como os he contado en mi entrada anterior "Calendario Matemático... (Portada)" aquí os dejo la hoja del calendario de noviembre, y un enlace a la web donde está también (en grande y para que descargueis) el calendario: noviembre.

Calendario Matemático... (Portada)

¡Matemáticas CADA DÍA!

A todos los profesores o alumnos de Eso o Bachiller y a todos los que les vayan los retos matemáticos os presento el Calendario Matemático, que cada año publican la Sociedad de Educación Matemática de la Comunidad Valenciana Al-khuarizmi (http://www.semcv.org/) y la editorial SM.

En el concurso del calendario (porque hay un concurso) solo pueden participar los alumnos de Eso y Bachiller con la supervisión de sus profesores. La información, requisitos, premios y los calendarios los teneis aquí: calendario matemático. A los que no podeis participar os invito igualmente a que resolvais alguno de los problemas de cada día, hay algunos cuanto menos, curiosos. Y otros que seguro rondarán en vuestra cabeza durante días.

Aquí os dejo la portada. Cada mes os colgaré también en el blog el calendario del mes.

El CALENDARIO MATEMÁTICO me lo presentó mi profesora de mates del instituto Virtu, la mujer que con su pasión por las matemáticas me hizo descubrir a mí mi pasión por ellas...

¡No olvide antes de leer la entrada concursar en la anterior!

“Hola, soy Monty Hall, tal vez me recuerde de películas como “21 blackjack”, y también de libros como “el curioso incidente del perro a media noche” o tal vez de series como “friends”. Aunque más probablemente me recuerde del concurso en el que empezó a participar ayer..

¿Se ha decidido? ¿Cambia usted de puerta?

Le revelo si usted ha hecho bien…”

 

Aquí os dejo el fragmento de la película “21 blackjack” (minuto 1 del video) en el que se hace referencia al famosísimo PROBLEMA DE MONTY HALL, el cual ha generado un intenso debate, debido a que la respuesta correcta parece contradecir conceptos básicos de probabilidad. La respuesta se basa en suposiciones que no son obvias y que no se encuentran expresadas en el planteamiento del problema, por lo que también se puede considerar como una pregunta con trampa.

 

Os dejo también otro vídeo que es un poco más explicativo y por si queda alguna duda al final de la entrada (*) os dejo mi explicación (hay diferentes maneras de explicar la respuesta).

 

 

Cualquier duda hay mucha información sobre este problema en Internet o pregúntame a mí.

 Os cuento también que en el capítulo 101 del libro “El curioso incidente del perro a medianoche” (2003), Christopher recurre al problema de Monty Hall para demostrar que la intuición puede hacer que nos equivoquemos, mientras que la lógica puede ayudarnos a deducir la respuesta correcta.

 En un episodio de la serie “Friends”, Chandler Bing hace referencia a Monty Hall en la cena previa a la boda de Ross Geller y Emily Waltham, cuando hace lo que él llama un "brindicito".

 

* Mi explicación: 

En el siguiente cuadro vemos las posibilidades que tenemos al elegir una puerta:

(puerta con cabra, puerta con cabra, o puerta con coche) y vemos también que pasa con cada puerta si cambiamos o no:

 Observamos que cambiando de puerta 2 de cada tres veces nos llevamo el coche (probabilidad del 66%), mientras que al no cambiar sólo 1 de cada tres veces nos llevamos el coche (probabilidad del 33,3%)

Si cambias ¡Tienes el doble de probabilidad de ganar el coche!

 

Así que enhorabuena a Joselito, Sonia y Laura. ¡Estefanía, a la próxima será!

¡Enhorabuena, es usted nuestro concursante!

¡Bienvenido al concurso de las 3 puertas! En el que usted puede ganar un fabuloso coche.

Usted debe elegir una puerta de entre tres, y se llevará lo que haya tras ella.

Detrás de una de ellas se encuentra el fantástico coche ya mencionado, y tras las otras una cabra salvaje (una detrás de cada puerta). Ya ve usted que no se va con las manos vacías.

¡Vamos! Elija una puerta.

 

¿Qué puerta ha elegido?

 

El famoso presentador que sabe qué hay detrás de cada puerta le abre una distinta a la que usted había elegido, y tras ella hay una cabra.

  

(Si usted había elegido la puerta 3 imagínese que la que está abierta es otra)

Y ahora le pregunta, ¿Quiere usted cambiar de puerta?


Responda en forma de comentario en el blog.



Y aquí la pregunta matemática, ¿Debe cambiar o quedarse con la puerta original? ¿Hay alguna diferencia? ¿Qué nos dice la probabilidad?

Tiene 1 día para pensarlo.
Mañana, la respuesta y el regalo.

Continuamos con la "magia" de Google...

Supongamos que después de una dura jornada llegas a casa y decides que necesitas desconectar y sumergirte en el mundo de algo que te apasione, por ello enciendes tu ordenador e inmediatamente  introduces en la barra de Google las palabras mágicas <<Justin Bieber concierto>>, pues bien, Google te ordena 11.400.000 resultados en 0,40 segundos. Por supuesto puedes hacer un doctorado sobre la vida de Justin Bieber, o saber cuántas novias ha tenido o incluso averiguar cada cuanto tiempo va tu querido Justin al baño. Pero tú solo quieres saber dónde será su próximo concierto. Google te facilita refinar tu búsqueda y acabar encontrando (rápidamente) lo que quieres.

Para ello tiene en cuenta al ordenar sus páginas (asignar el peso a cada página) los siguientes aspectos: No es lo mismo que un cierto término aparezca en una página en el título, en negrita, o en un tipo de letra pequeña. Tampoco es lo mismo que los términos buscados aparezcan “cerca” o “lejos” unos de otros. Tiene también en cuenta el número de visitas que la web ha recibido, así como las webs que tienen une enlace a dicha página, y cómo de importantes son estas páginas que la enlazan.

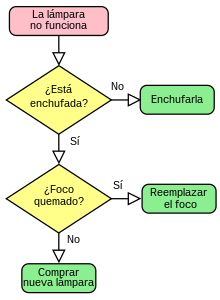
Todo esto, lo calcula rápidamente a través de un algoritmo, que es “un conjunto preescrito de instrucciones o reglas bien definidas, ordenadas y finitas que permite realizar una actividad mediante pasos sucesivos que no generen dudas a quien deba realizar dicha actividad”. Veamos un ejemplo sencillo de algoritmo:

 

 

El algoritmo con el que asigna Google las importancias y ordena las páginas es un algoritmo lleno de matemáticas. Para entenderlo bien se necesitan los conocimientos de un tercer curso de carrera de la licenciatura más o menos. Voy a intentar daros una idea sencilla, pero a todos los que os atreváis a indagar un poco mas en este tema os “súper-recomiendo” el siguiente artículo que podéis encontrar en Internet “El secreto de Google y el álgebra lineal” de Pablo Fernández Gallardo.

Para tener una ligera idea del funcionamiento del algoritmo vamos a suponer que solo consideramos importante cuántas páginas enlazan a la web a la que queremos asignar el peso, y supondremos también que solo tenemos tres webs en Internet. Y esto nos dará una ligera  idea de lo que pasa en toda la red .

 

Tenemos las siguientes páginas relacionadas tal y como muestra el dibujo:

La página 3 tiene un enlace a la página 1 y 2, y la página 2 tiene un enlace a la página 1.

Calculamos entonces los pesos de cada página del siguiente modo:

Peso1=  1/2 + 1= 3/2  (El 1/2 representa que le llegan 1 enlace de 2 que hay en la página 3, y el 1 que le llega un enlace de 1 que hay en la página 2).

 

Peso 2= 1/ 2 (Llega un enlace de 2 que hay en la página 3)

Peso 3=0 (No le llegan enlaces)

Por tanto el orden en que Google nos mostraría las páginas sería: 1. Web oficial de Justin Bieber, 2.Web de conciertos de Justin, y 3. Web de prensa rosa.

Pero esto... es sólo el principio... Si quieres más, ya sabes... “El secreto de Google y el álgebra lineal” de Pablo Fernández Gallardo.

¿Magia en Google?

 

 

Google, Yahoo, msn search, bing, ask, blekko, altavista, trovator, lupa… ¿Será por buscadores en Internet?

Pero seguro que si preguntase, la mayoría de nosotros sin ninguna duda seríamos Google-adictos.

Pero…¿Por qué si hay tantos buscadores nosotros adoramos a Google y no nos imaginaríamos (ni queremos imaginarnos) Internet sin él? ¿Por qué es Google nuestro dios de los buscadores?

La respuesta a estas preguntas es muy sencilla… POR CÓMO ORDENA LOS RESULTADOS DE NUESTRAS BÚSQUEDAS.

 Nuestros queridos Brin y Page, al crear Google se plantearon un objetivo, y es que, en un número suficientemente grande de los casos, al menos una de, digamos, las diez primeras páginas que se muestren contenga información útil para el que realiza la consulta. Pido ahora al lector que decida, a partir de su experiencia personal, si Google cumple este objetivo. Estoy segura de que la respuesta general es que sí, y de manera asombrosa. Parece magia… pero son MATEMÁTICAS. Adentrémonos en ellas.

 Brin y Page necesitaban un criterio de ordenación. Para ello a cada página de Internet asignan un peso (un número) que nos indica cómo de importante es esa página. De manera que tenemos una lista (interminable) de webs con unos números que nos indican la importancia de cada una de estas webs. Así, cuando nosotros introduzcamos nuestras palabras a buscar en la barra de Google, este seleccionará de la lista las webs en las que aparezcan nuestras palabras y nos las mostrará ordenadas según la lista anterior, es decir, según su peso.

 

Pero… ¿Cómo se asignan esos pesos a cada página? ¿Qué tiene en cuenta para decir cómo de importante es una página? ¿Cómo hace esto con el increíble número de páginas que hay en Internet?

Todas estas respuestas y mucha "magia" más, en mi próxima entrada...

¿Y a ti qué te pasa...?

 TODOS tenemos una "relación" con las matemáticas... Una relación de amor... O tal vez una relación de odio.. Quizás sea un romance que acabó y no queramos ni volver oír hablar de él... Igual le tenemos miedo.. O probablemente sea una historia que tuvo que acabar pero que en lo más profundo de nosotros deseamos retomarla...
Pero una cosa está clara... Las matemáticas no dejan indiferente a NADIE...

El siguiente fragmento de la presentación del libro Vitaminas Matemáticas de Claudi Alsina nos puede ayudar a ver cual es nuestra historia con los números antes de adentrarnos en ellos, y a mi, me ayudará a contaros un poco más cuál es mi propósito con este blog...

"Todos tenemos una cita pendiente con las matemáticas. Pero en este fantástico reencuentro, como en la vida amorosa de verdad, pueden concurrir diversas circunstancias.

La primera posibilidad es que usted ya haya logrado uno o diversos divorcios con las matemáticas, después de discusiones tensas y largas separaciones temporales. Posiblemente su relación empezó bien (usted era muy joven), pero hubo un día en que le obligaron a aprender la resta llevando, usted empezó a dudar y diversas malas experiencias docentes fueron enturbiando su relación con la disciplina. En este caso posiblemente usted protagonizó un abandono de hogar precipitado y desde el ahí te quedas  usted va proclamando por el mundo su clara vocación por las letras.Si éste es su caso, este libro intentará, como mínimo un acercamiento amable y que a través de esta nueva cita matemática pueda darse una reconciliación. (...)

La segunda posibilidad es que usted no se haya divorciado aún de las matemáticas pero ya tenga en marcha los trámites de separación. En este caso usted aún mantiene acaloradas discusiones (¿y para  qué sirven?, ¿y yo qué saco de esto?...) o mantienen un frío alejamiento (¡me producen sueño!, ¡qué aburridas!...). En tal circunstancia el libro intentará seducirle para que vuelvan a tener una bella relación, como al principio. (...)

La tercera posibilidad es la óptima. A usted le encantan sus citas matemáticas e incluso manifiesta en público su cariño por ellas. Entonces las vitaminas le permitirán reafirmar su reconocida condición de alma pitagórica. (...)"

En mi opinión el odio a las matemáticas viene producido por el no haber dedicado suficiente tiempo a conocerlas... Si realmente con tiempo las descubres, puedes disfrutar más o menos de ellas, pero la satisfacción que produce la resolución de un problema después de un largo "calentamiento de cabeza" y la belleza de ver que todo encaja no nos permite odiarlas...

... ¿Te atreves a DESCUBRIRLAS?

...así ¿Cómo?

Las matemáticas CONTADAS bonitas..

¡Revelaremos sus secretos más ocultos y sus historias y aplicaciones más curiosas!
CONTAREMOS los números y la belleza de estos de modo que nos hagan disfrutar de ellos.
Muchas veces las cosas nos atraen o no dependiendo de la forma en la que se CUENTEN.. ¡ Tal vez, CONTADO ASÍ...  todo cambie! ¡Hasta TU historia con ellas!

Un blog que pretende engancharTE y sorprenderTE a través del CUENTO  de las matemáticas...